
When combining transformations, it is very important to consider the order of the transformations. Write a formula for the toolkit square root function horizontally stretched by a factor of 3.
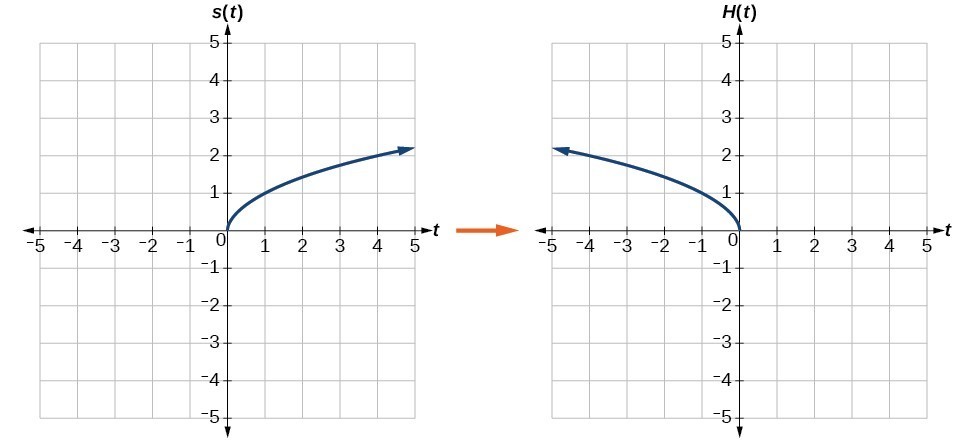
Figure 19 shows a function multiplied by constant factors 2 and 0.5 and the resulting vertical stretch and compression. If the constant is greater than 1, we get a vertical stretch if the constant is between 0 and 1, we get a vertical compression. When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. Each change has a specific effect that can be seen graphically. We can transform the inside (input values) of a function or we can transform the outside (output values) of a function. We now explore the effects of multiplying the inputs or outputs by some quantity. Is the function f ( s ) = s 4 + 3 s 2 + 7 f ( s ) = s 4 + 3 s 2 + 7 even, odd, or neither? Graphing Functions Using Stretches and CompressionsĪdding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect the shape of a graph. For a function g ( x ) = f ( x ) + k, g ( x ) = f ( x ) + k, the function f ( x ) f ( x ) is shifted vertically k k units. In other words, we add the same constant to the output value of the function regardless of the input. The simplest shift is a vertical shift, moving the graph up or down, because this transformation involves adding a positive or negative constant to the function. One simple kind of transformation involves shifting the entire graph of a function up, down, right, or left. There are systematic ways to alter functions to construct appropriate models for the problems we are trying to solve. One method we can employ is to adapt the basic graphs of the toolkit functions to build new models for a given scenario. Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs, and equations. Graphing Functions Using Vertical and Horizontal Shifts In this section, we will take a look at several kinds of transformations. In a similar way, we can distort or transform mathematical functions to better adapt them to describing objects or processes in the real world.
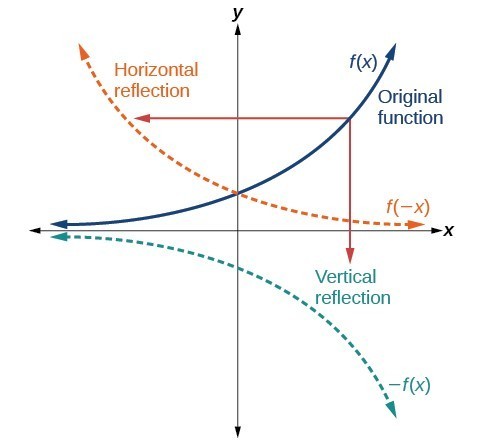

But what happens when we bend a flexible mirror? Like a carnival funhouse mirror, it presents us with a distorted image of ourselves, stretched or compressed horizontally or vertically. When we tilt the mirror, the images we see may shift horizontally or vertically. We all know that a flat mirror enables us to see an accurate image of ourselves and whatever is behind us.


 0 kommentar(er)
0 kommentar(er)
